Introduction

TensorLDA uses tensor decomposition method to estimate parameters in a Latent Dirichlet Allocation model. This introduction will focus on how to learn LDA parameters with tensor decomposition method.

LDA Parameters

First, we define LDA parameters:

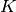  • K : number of topics
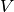  • V : vocabulary size
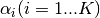  • \alpha_i (i = 1...K) : dirichlet prior for topic i
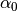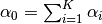  • \alpha_0 : sum of topic priors (\alpha_0 = \sum_{i=1}^{K} \alpha_i)
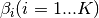  • \beta_i (i = 1...K) : word distribution for topic i

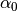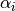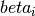In the model we assume \alpha_0 is given and our goal is to estimate \alpha_i and beta_i from a given corpus.

Data Moments

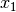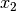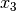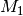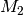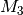Since the model is based on decomposition of third order tensor, another assumption here is each document contains at least 3 words. Let x_1, x_2, and x_3 be any triple of words in a document, the first three order data moments M_1, M_2, and M_3 are defined as:

M_1 = & \mathop{\mathbb{E}}[x_1] \\ M_2 = & \mathop{\mathbb{E}}[x_1 \otimes x_2] - \frac{\alpha_0}{\alpha_0 + 1} M_1 \otimes M_1 \\ M_3 = & \mathop{\mathbb{E}}[x_1 \otimes x_2 \otimes x_3] \\ & - \frac{\alpha_0}{\alpha_0 + 2} ( \mathop{\mathbb{E}}[x_1 \otimes x_2 \otimes M_1] + \mathop{\mathbb{E}}[x_1 \otimes M_1 \otimes x_3] + \mathop{\mathbb{E}}[M_1 \otimes x_2 \otimes x_3]) \\ & + \frac{\alpha_0^2}{(\alpha_0 + 2)(\alpha_0 + 1)} M_1 \otimes M_1 \otimes M_1

Based on dirichelet priors, we can derive the relationship between data moments and model parameters as:

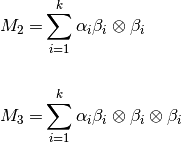
M_2 = & \sum_{i=1}^{k} \alpha_i \beta_i \otimes \beta_i \\ M_3 = & \sum_{i=1}^{k} \alpha_i \beta_i \otimes \beta_i \otimes \beta_i

Whitening

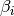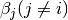As we know \beta_i and \beta_j (j \neq i) are not necessary orthogonal, the deccomposition of 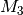M_3 may not be unique. Therefore, we need to orthogonize 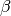\beta first.

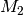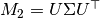To do this, we find orthogonal decomposition of M_2 where M_2 = U \Sigma U^\top. Then we can define whitening matrix 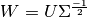W = U \Sigma^{\frac{-1}{2}}. And since 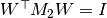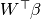W^\top M_2 W = I, W^\top \beta is orthogonal.

The thrid order tensor after whitening is:

T =& \mathop{\mathbb{E}}[W^\top x_1 \otimes W^\top x_2 \otimes W^\top x_3] =& \sum_{i=1}^{k} \alpha_i^{\frac{-1}{2}} (W^\top \beta_i \alpha_i^{\frac{1}{2}}) \otimes (W^\top \beta_i \alpha_i^{\frac{1}{2}}) \otimes (W^\top \beta_i \alpha_i^{\frac{1}{2}}) =& \sum_{i=1}^{k} \lambda_i \nu_i \otimes \nu_i \otimes \nu_i

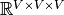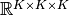Another advantage of whitening is dimension reduction. After whitening, the tensor dimension is reduced from \mathbb{R}^{V \times V \times V} to \mathbb{R}^{K \times K \times K}.

Tensor Decomposition

Currently we implemented “Robust tensor power method” described in Reference [1]. Assuming tensor 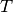T is orthogonally decomposable, we can estimate one (eigenvalue, eigenvector) pair with power iteration update. Once a pair (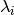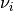\lambda_i, \nu_i) is found, we deflate tensor 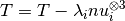T = T - \lambda_i nu_i^{\otimes 3} and compute the next (eigenvalue, eigenvector) pair. For details, check algorithm 1 in reference [1].

Parameter Reconstruction

Once we get all 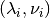(\lambda_i, \nu_i) pair, reconstruction is simple:

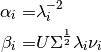
\alpha_i =& \lambda_i^{-2} \beta_i =& U \Sigma^{\frac{1}{2}} \lambda_i \nu_i

References: